Given a sorted array of size N and an integer K, find the position at which K is present in the array using binary search.

SOLUTION:

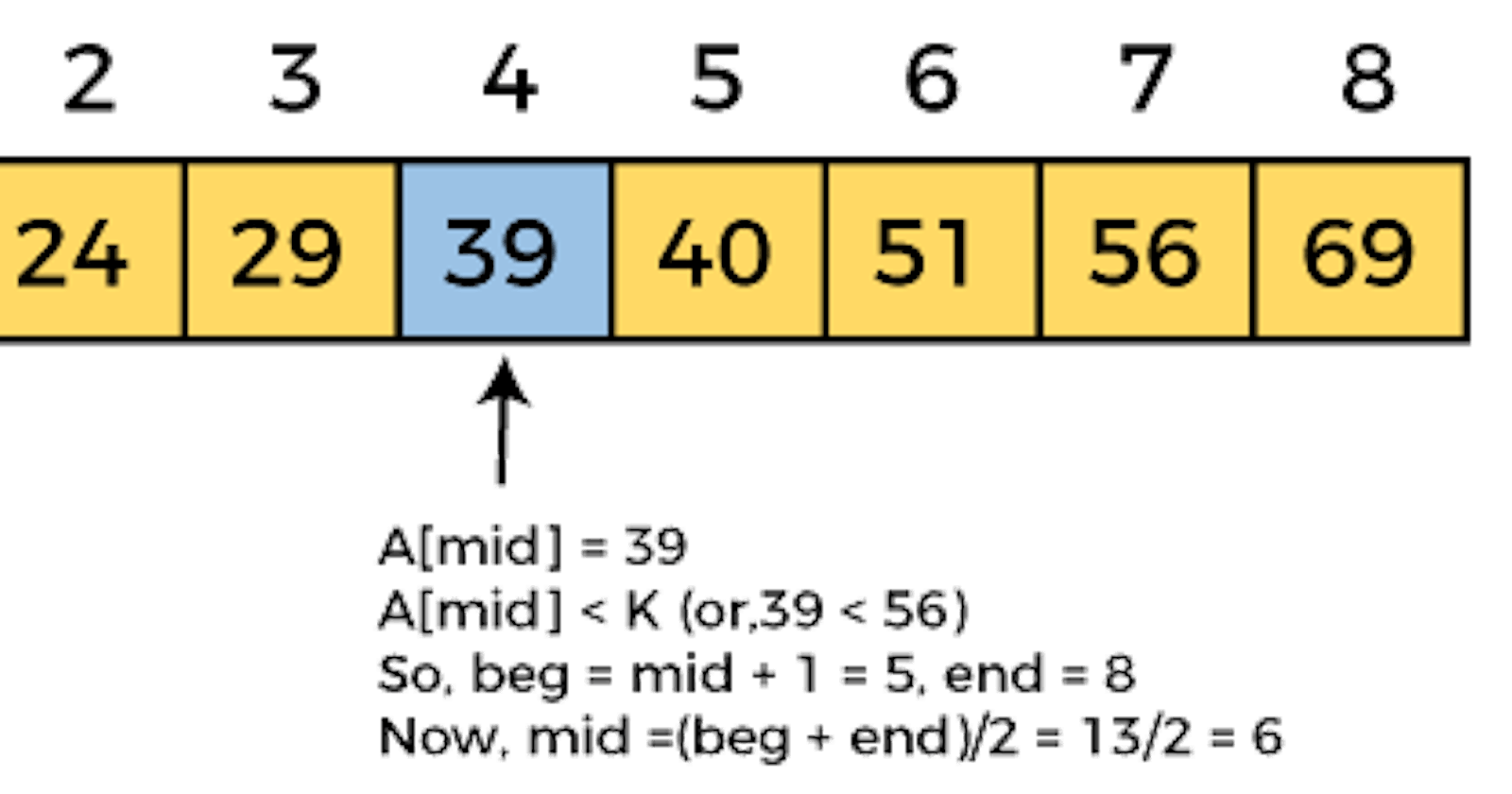
Binary search divides the input array by half at every step. After every step, either we find the index we are looking for, or we discard half of the array.

• - At each step, consider the array between low and high indices.

• - Get a middle index: mid.

• - Compare mid to K, if equal to K return mid index.

• -If mid > K, Change the index high to mid - 1, low remains the same

• - if mid < k, Change low to mid + 1. high remains the same

  class Solution {
    int binarysearch(int arr[], int n, int k) {
        // code here
        int low = 0;
        int high = n-1;
        while (low <= high) {
            // Finding the mid using floor division
            int mid = low + ((high - low) / 2);
  
            // Target value is present at the middle of the array
            if (arr[mid] == k) {
                return mid;
            }
  
            // Target value is present in the low subarray
            else if (k < arr[mid]) {
                high = mid - 1;
            }
  
            // Target value is present in the high subarray
            else if (k > arr[mid]) {
                low = mid + 1;
            }
        }
  
        // Target value is not present in the array
        return -1;
  
    }
  }
  

  Time complexity The time complexity of this solution is logarithmic, O(log \space n) O(log n) .

Space complexity The space complexity of this solution is constant, O(1) O(1) If you have a better solutoin you can drop it in the comments.